新型コロナウイルスに限らず、感染症の今後の状況などを予測するのに、数理モデルが良く使われています。
感染が拡散し収束していく状況を示すものですね。
その感染症の数理モデルも様々であるけれど、条件を狭めて簡略化すれば、Excelとそのマクロでもできるので、かなり簡単な条件で計算してみました。
かなりおおざっぱだけれども、感染が広がっていく様子は、なかなか興味深い結果だと思います。
計算条件
一応、新型コロナウイルス(Covid-19)を想定し、以下の条件で行いました。
かなり、ざっくりと簡略化しています。
・12Periodで完結するよう期間設定。
・要素は20×20の400とし、ランダムで数十ケース計算した平均値としています。
・基本再生産数の取り方が微妙なのだけれど、何度かトライアルで3程度となるように調整。
・感染者の回復期間は平均2週間から推定。
・当然のことながら、変性は考慮していないし、死者もないものとしています。
色は以下の通りです。
S:感染可能性のある者(薄緑色)
I:感染者(オレンジ色)
R:回復者(青色)
いわゆる、今の未感染の私たちがSに該当します。
そもそも、感染の拡大と収束のイメージをつかむだけの計算結果ですので、よくわからなくて構いません。
図の色だけは覚えてご覧ください。
計算結果
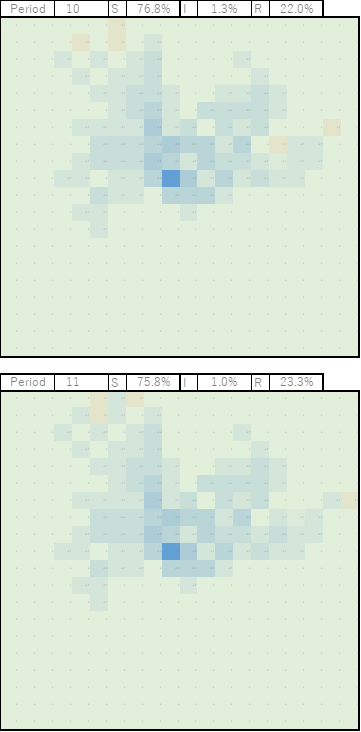
クラスター1地点のケース
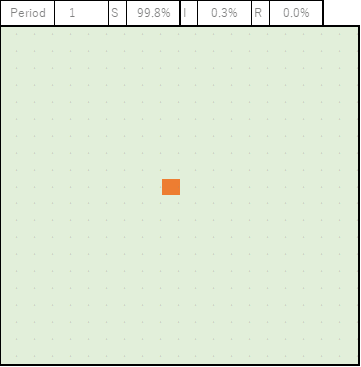
じわじわとオレンジ(感染者I)が増えていきます。

オレンジ色が広範囲に広がっていきますが、中央部は青色(回復者R)も増えていきます。
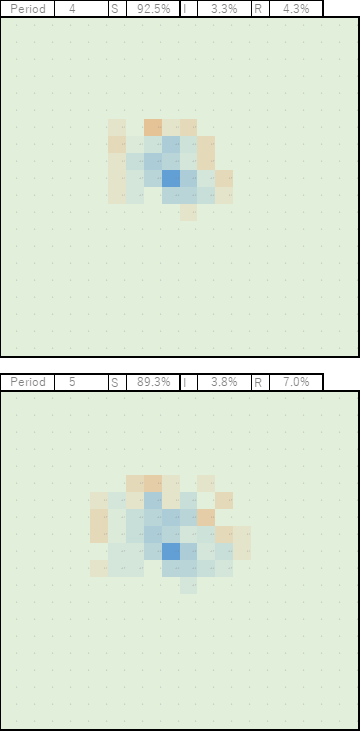
色は薄いですが、かなりの広範囲に広がっていきます。
今回のケースでは、このPeriodが最も多い感染者数となりました。
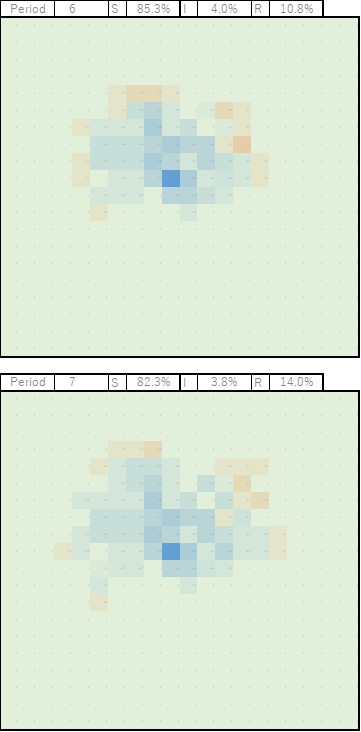
このあたりから減少します。
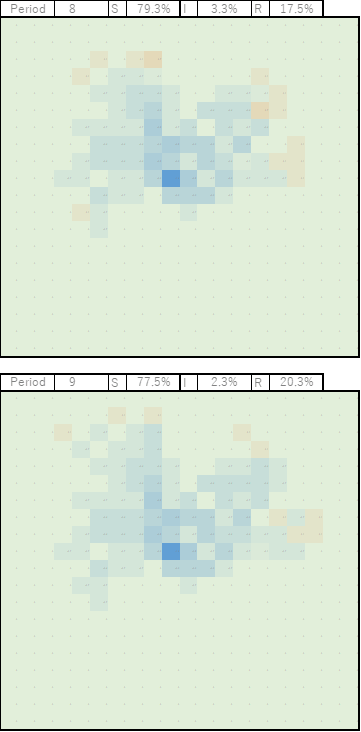
次第に回復者がかなり増えてきますが、感染者の減少速度が意外に遅い。
この辺りまでくれば、社会的影響も少ないのでしょうが、完全制圧までの詰めの一手が長引くのかもしれません。
やがて、このケースでは全体の24.3%が感染して回復という結果になりました。
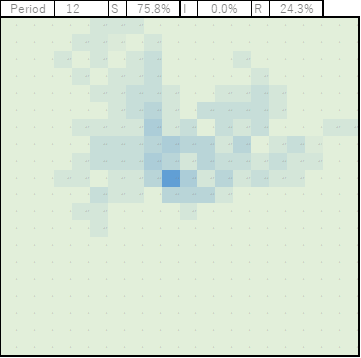
こうやって実際に計算してみると、想像以上に広範囲に影響することがわかる。
また、感染拡大の期間より、減少期間の方がだらだらと長引く傾向にあるようです。
感染者が減り始めたからと油断するのは禁物ということでしょうか。
ただし、このモデルの弱いところは人の動きを考慮していないこと。
クラスターが移動、いわゆる感染者Iが非感染者Sの割合が大きい領域に入り込むとかなり大変。
そのため、移動制限が有効になるのである。
そんな事態になっても、必ず収束していくので耐えましょう。
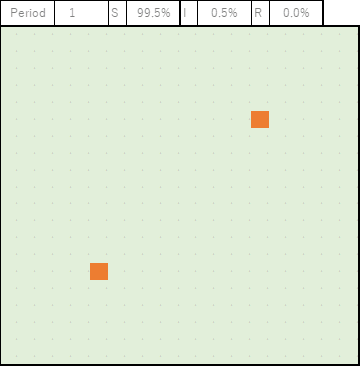
クラスター2地点のケース
2地点でクラスターがあったケースもざっと示しておきます。
これもなかなか興味深い結果に。
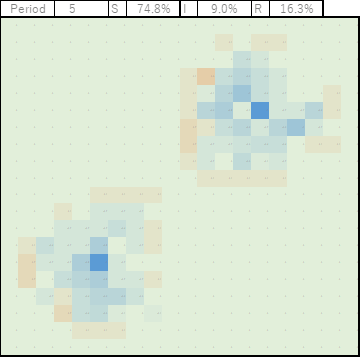
Period5
オレンジ色の感染者がじわじわと広がっていきます。
Period9
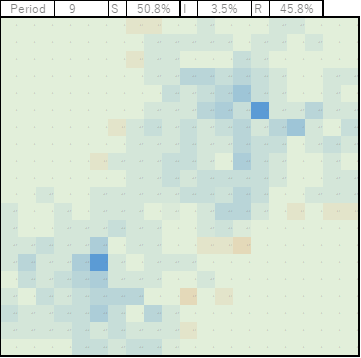
このあたりになると、両方のクラスターがくっつきます。
青色(回復者R)に囲まれた薄緑色(非感染者S)の領域も結構あります。
おそらくこのあたりが、イギリスの首相やドイツのメルケル首相が集団免疫とか人の壁とか言っていた部分でしょう。
Period12
ちょっと残っているけれど、ほぼオレンジが消えたのでこのあたりで止めました。
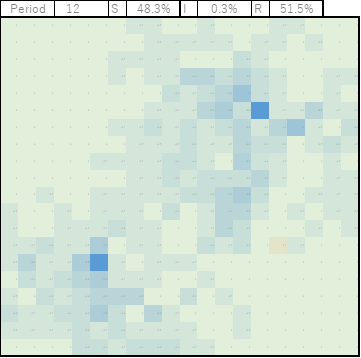
欧州でしきりに出ていた、免疫を獲得したものが壁になって食い止めるという考え方。人の壁、集団免疫を獲得するには、やはり感染者も50%以上にはなるようですが、あながち間違いではないような気もします。メルケル首相は60~70%が感染するって言ってましたよね。
ただし、この考え方は感染爆発をすると医療崩壊して、元も子もなくなる。
ゆっくりと感染者が増える分には意外と有効なのかもしれません。
おわりに
ここで計算したものはあくまでもざっくりとした試算です。
公表されるようなものは、もっと細かいパラメータースタディー、キャリブレーションを行って、とんでもない量の繰り返し計算をして算出していると思うの、こんなに簡単な話ではありません。
感染が広がり、また収束していくイメージをみんなが共有し、有効な治療法ができるまでは、長く地道な戦いになるかもしれないということを共有できれば幸いです。